FIT CTU

Adam Vesecký

NI-APH
Lecture 8

APHGames.io

Physics

Literature

Millington, Ian. Game Physics Engine Development

Geometry

Points and Vectors

  • Cartesian coordinate system - by far the most common
  • games usually use Euclidean space
  • in 2D engines, Y-axis is usually inverted

2D coordinate system

3D coordinate system

Points and Vectors

  • Vector - a quantity that has both a magnitude and a direction
  • vector can be used to represent a point, provided that we fix the tail of the vector to the origin of the coordinate system

Addition and subtraction

  • vector + vector = vector
  • vector - vector = vector
  • point + vector = point
  • point - point = vector
  • point + point = undefined

Vector addition and subtraction

Points and Vectors

Magnitude

  • scalar representing the length of the vector
  • |a| = \sqrt{a_x^2+a_y^2+a_z^2}

Magnitude of a vector

Normalization

  • a unit vector is a vector with a magnitude of one: \mathrm{u} = \frac{\mathrm{v}}{|\mathrm{v}|}

Normal vector

  • vector is normal to a surface if it is perpendicular to it

Dot product

  • \mathrm{a}\cdot\mathrm{b} = a_xb_x+a_yb_y+a_zb_z
  • \mathrm{a}\cdot\mathrm{b} = |\mathrm{a}|\cdot |\mathrm{b}|\cdot \cos{(\theta)}

Cross product

  • yields another vector that is perpendicular to two vectors
  • \mathrm{a}\times\mathrm{b} = [(a_yb_z - a_zb_y),(a_zb_x - a_xb_z),(a_xb_y - a_yb_x)]

Projection

  • projection of a vector onto another vector
  • \mathrm{v'} = \frac{\mathrm{w}\cdot\mathrm{v}}{|\mathrm{v}|^2}\cdot \mathrm{v}

Dynamics

Terms

  • Kinematics - determines motion of objects without reference to forces
  • Dynamics - determines how objects interact under the influence of forces
  • Time - a continuous progress of events, measured in seconds
  • Mass - a scalar quantity measured in kilograms
  • Position - a point or an area occupied by an object
  • Velocity - the rate of change of distance over time
  • Acceleration - the rate of change of velocity over time
  • Force - an action exerted upon a body in order to change its state
Most engines use MKS units (meters, kilograms, seconds) and radians for angles.

Dynamics

Linear Dynamics

  • we ignore all rotational effects
  • position can be described by a position vector \mathrm{r}
  • velocity: v(t) = \frac{dr(t)}{dt}
  • acceleration: a(t) = \frac{dv(t)}{dt} = \frac{d^2r(t)}{dt^2}
  • net force: \mathrm{F_{net}} = \sum^N_{i=1} \mathrm{F_i}
  • Newton's second law: \mathrm{F} = m\cdot a(t)
  • linear momentum: \mathrm{p(t)} = m\cdot v(t)

Angular dynamics

  • angular velocity: \omega(t) = \frac{d\varphi(t)}{dt}
  • angular acceleration: \alpha(t) = \frac{d\omega(t)}{dt} = \frac{d^2\varphi(t)}{dt^2}
  • torque: \mathrm{N} = \mathrm{r} \times \mathrm{F} , caused by a force applied to a location
Any physical behavior of an object can be decomposed into linear motion of the center of mass and angular motion around the same point

Motion

Projectile motion

  • \mathrm{F} = m\cdot \mathrm{a}
  • m\cdot \mathrm{a} = -m\cdot \mathrm{g}
  • \mathrm{a} = -\mathrm{g}

Slope motion (no friction)

  • \mathrm{F} = m\cdot \mathrm{a}
  • \mathrm{F} = \mathrm{F_G} \cdot \sin{(\alpha)}
  • \mathrm{a} = \frac{\mathrm{F}}{m} = \mathrm{g}\cdot \sin{(\alpha)}

Equations of motion

  • finding v(t), r(t) , given knowledge of \mathrm{F_{net}}(t)
  • vertical motion under the influence of gravity
    • r''(t) = g
    • r'(t) = g\cdot t + v_0
    • r(t) = \frac{1}{2} \cdot gt^2 + v_0t + r_0
    • too difficult - with any change of any force, we would need to modify the simulation code
    • analytical solutions are almost never possible in game physics
  • Numerical integration
    • given r(t_1), v(t_1), \mathrm{F}(t, r, v) , the problem is to find r(t_2), v(t_2)
    • we will start at r(t_1)  and take steps in time along
      the tangent, until we generate an approximation for r(t_2)
    • integration methods provide us with the possibility of
      an approximation with increasing precision

Integration Methods

Implicit methods

  • make use of quantities from the next time step
  • decrease energy from the system

Explicit methods

  • make use of known quantities at each time step

Semi-implicit methods

  • combination of explicit and implicit methods
  • very stable

Runge-Kutta family

  • Euler methods, midpoint methods, RK4,...

Verlet family

  • Regular Verlet
  • Leapfrog Verlet
  • Velocity Verlet

Euler Integration

  • v(t+ \Delta t) = v(t) + a(t) \cdot \Delta t

Explicit method

  • r(t+\Delta t) = r(t) + v(t) \Delta t

Improved method

  • r(t+\Delta t) = r(t) + \frac{v(t)+v(t+\Delta t)}{2} \Delta t

Implicit method

  • r(t+ \Delta t) = r(t) + v(t+\Delta t) \Delta t
  • cheap and easy to implement
  • high error and poor stability, depending
    directly on the time step

Steering Behaviors

Steering Behaviors

  • a set of algorithms that help autonomous agents move in a realistic manner by using simple forces
  • designed by Crag Reynolds in the early 90's
  • Agent - a system situated within an environment, with the ability to sense that environment
  • Motion layers
    • action selection - choosing goals, strategy
    • steering - trajectory calculation
    • locomotion - way of moving, animation, articulation

Steering Behaviors

Seek

  • the simplest steering behavior
  • a force that directs an agent toward a target position

Steering Behaviors

Flee

  • opposite of seek, creates a force that steers the agent away

Arrive

  • seek + stopping movement, decelerates the agent onto the target

Pursuit

  • agent intercepts a moving target
  • predicts where the target is going to be in the future
  • calls for a good prediction function

Evade

  • opposite of pursuit
  • the evader flees from the estimated future position

Steering Behaviors

Wander

  • produces a force that will give an impression of a random walking
  • small random displacement is applied to the velocity vector every frame
  • a circle is projected in front of the vehicle
  • the vehicle is steered toward a target that moves along the perimeter
  • parameters: circle radius, distance from the vehicle and jittering (randomness)

Steering Behaviors

Path follow

  • moves a vehicle along a set of waypoints
  • the last waypoint can be reached using arrive, the others via seek
  • smooth movement can be achieved using a tolerance radius or Bézier curve approximation
  • very sensitive to configuration (max force, max velocity, radius,...)

Steering Behaviors

Flocking

  • combination of three aspects:
    • separation - steers a vehicle away from its neighborhood
    • alignment - keeps the vehicle's direction aligned with its neighbors
    • cohesion - moves a vehicle toward the center of mass of its neighbors

Physics Engine

Physics engine

  • system that approximates physical phenomena in real-time
  • can improve immersion
  • can broke the game story
  • Flow

Physics Engines

N-Collide

  • 2D/3D collision detection library written in Rust

Box2D

  • open-source C++ 2D physics engine
  • supports CCD (continuous collision detection)

Bullet

  • open-source 3D physics engine
  • supports CCD

PhysX

  • NVidia GPU engine
  • PhysX destruction, PhysX clothing, PhysX particles

p2.js

  • module JavaScript engine, supports CCD

Havok

  • gold commercial standard

Physics and animation

  • physics \neq  animation!
  • animations must cooperate with physics engine to run seamlessly
  • cut-scenes and state-transition animations are detached from physics
  • physics-based interactions - animations generated by physics engine
  • almost all AAA games still use static animations connected to the physical environment

Physics engine features

  • collision detection
  • contact callbacks
  • joints
  • concave and convex hulls
  • compound bodies
  • sleeping objects
  • raycasting, shapecasting
  • deformable structures
  • destructible structures
  • trigger volumes
  • complex machines
  • drivable vehicles
  • rag doll characters
  • water surface, hair, cloth
  • particles

Physics in games

Pinballs (1980+)

  • non-trivial OBB collision detection

The Incredible Machine (1993)

  • advanced physical interactions

Worms (1995)

  • pixel-level environment interaction

Half-Life 2 (2004)

  • destructible environment, liquid physics

Physics in games

Angry Birds (2009)

  • physics as the core mechanic

INSIDE (2016)

  • soft-bodies driven by a network of impulses

Half-Life Alyx (2020)

  • physics-based interactions

Noita (2020)

  • pixel-level physics simulation

Object types

Body

  • fundamental object in the physics scene

Rigid Body

  • idealized, infinitely hard, non-deformable solid object
  • physics-driven bodies - driven entirely by the simulation
  • game-driven bodies - moved in a non-physical way (animations)
  • fixed bodies - collision-only bodies (e.g. triggers)

Soft body

  • deformable

Shape

  • region of space described by a boundary, with a definite inside and outside (curved line, polygon, curved surface, polyhedron)

Fixture

  • used to describe size, shape and material properties

Object Types

Constraint

  • connects bodies together in order to simulate interaction (ropes, wheels, vehicles, chains)

Sensor/Phantom

  • entity that provides a feedback when certain objects overlap
  • participates on collision detection but doesn't affect the scene

Rag doll

  • displays human-like figures with a realistic motion

Destructible object

  • breakable object, can be implemented by using rigid body dynamics, dividing the model into a number of breakable pieces

Constraints

  • Revolute - a hinge or pin, where the bodies rotate
    • wheels, chains, rotating doors, catapults, levers
  • Distance - a point on each body will be kept at a fixed distance apart
  • Rope - restricts the maximum distance between two points
  • Prismatic - body's motion is restricted to a single degree of freedom
    • elevators, sliding doors, pistons
  • Weld - holds the bodies at the same orientation
  • Cone-Twist - adds a cone and twist axis limits (6 degrees of freedom)
  • Gear - controls two other joints so that the movement of one affects the other
  • Motor - joint with torque or angular impulses

Constraints

rope

revolute

prismatic

cone-twist

Constraints

Fracturing

  • breaking an object into smaller fragments
  • in many cases destruction is not dynamic (can be made using animations)
  • techniques: manual fracturing, Voronoi Shattering, voxels

Paratrooper (1982)

Fictorium (2017)

Teardown (2020)

Particle Systems

  • a collection of point masses that obeys certain physical laws
  • can model complex fuzzy shapes and dynamics
  • uses Flyweight pattern (array of positions, velocities, group lists)
  • particles are not only moving points! Even a tree may become a particle

Applications

  • fluids
  • visual effects
  • flocks
  • rendered trails (plants)
  • soft bodies (flag, cloth)

Soft bodies and liquids

  • usually implemented as a combination of particle systems and visual effects
  • common model:
    1. apply collision detection upon particles
    2. apply pressure and repulsive forces
    3. update positions
    4. handle interaction with other objects

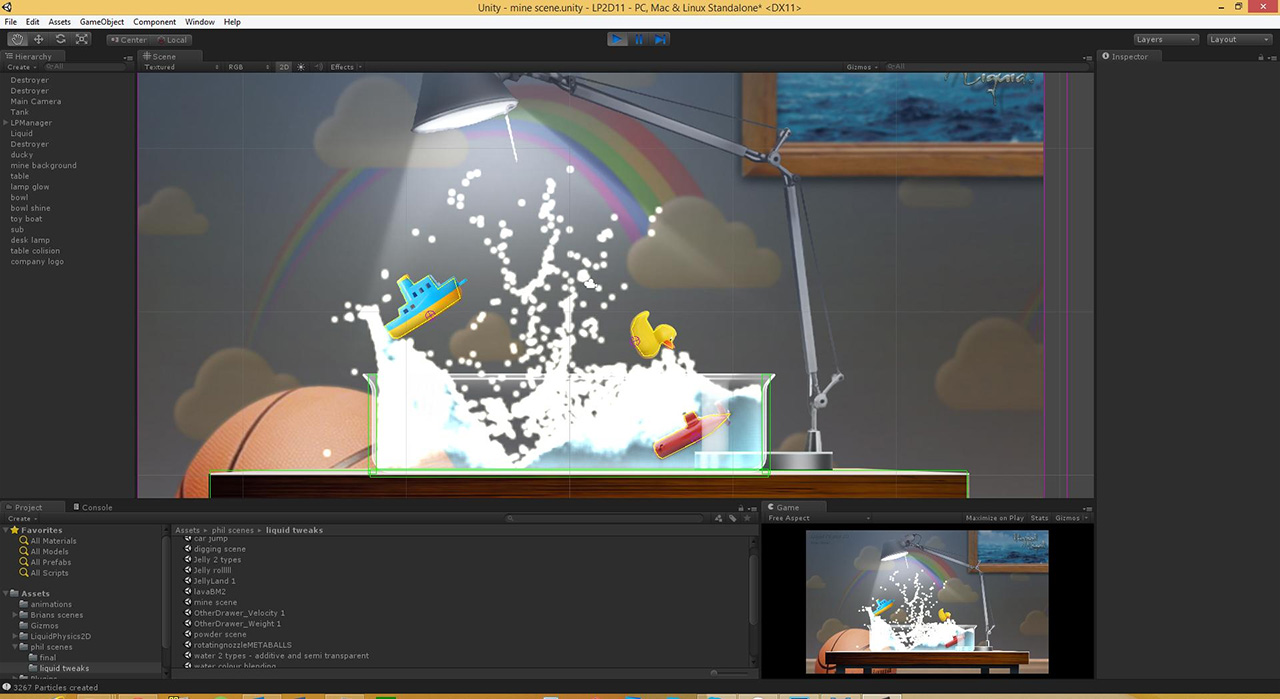
Example: CryEngine Fluid Physics

  • utterly complex
  • 5000+ lines of code for just the RigidBody part
  • very poor code quality
       1 if (min(min(min(body.M,ibody_inv.x),ibody_inv.y),ibody_inv.z)<0) {
    

       2 	body.M = body.Minv = 0;
    

       3 	body.Ibody_inv.zero(); body.Ibody.zero();
    

       4 }	else {
    

       5 	body.P = (body.v=v)*body.M; 
    

       6 	body.L = body.q*(body.Ibody*(!body.q*(body.w=w)));
    

       7 }

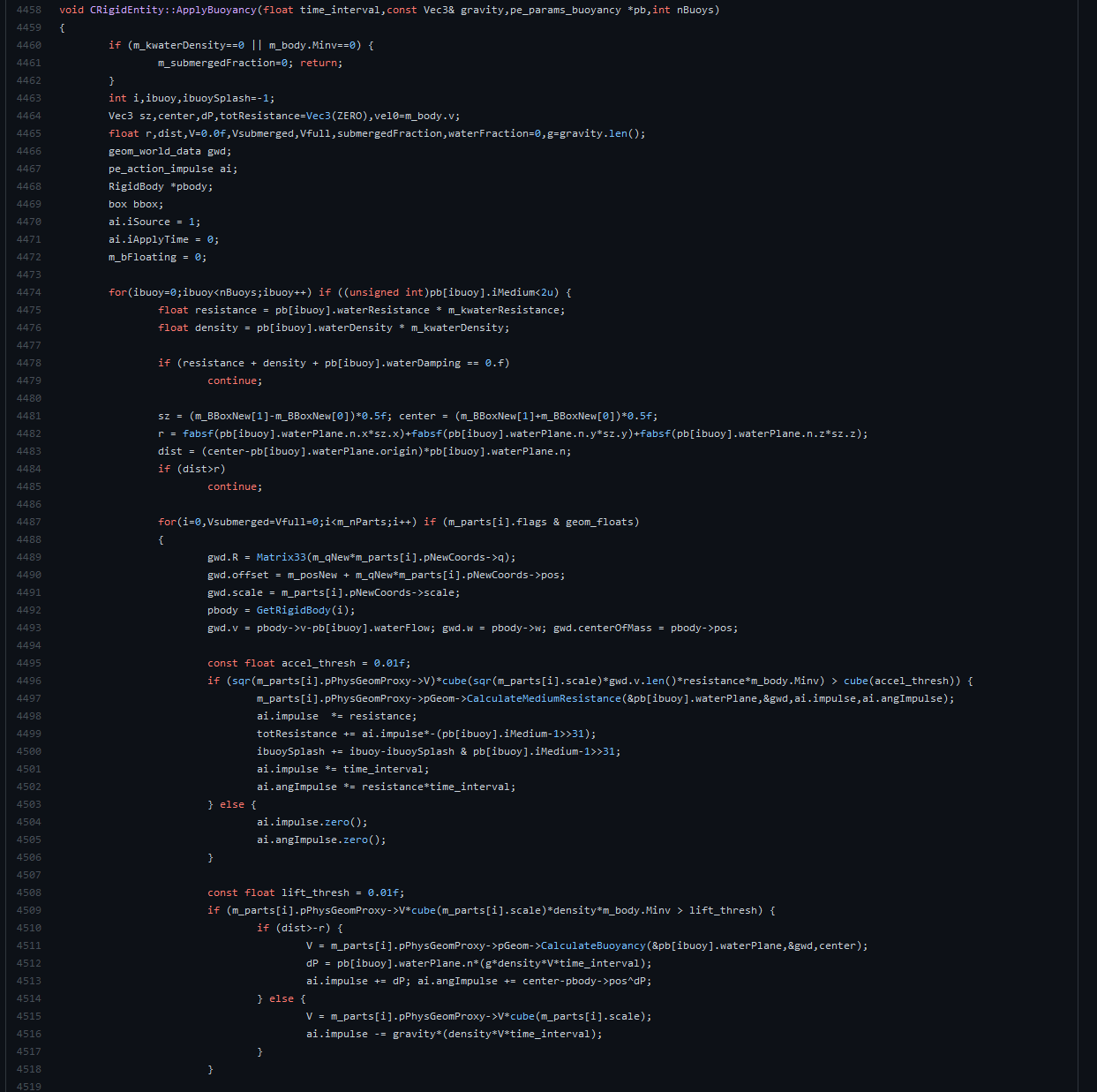
Collision Detection

Collision Detection

Steps

  • positions for the next frame are determined
  • a spatial data structure finds collision candidates
  • collision candidates are filtered out into a set of real collision pairs
  • collisions are resolved by the collision resolver, by applying impulses or penalty forces
  • constraints are satisfied by the constraint resolver

Collidable entities

  • we need to provide a collision representation for each object
  • simple shapes are preferred (a car might be modelled as a rectangle)
  • more-complex shapes should only be used when the simple ones provide inadequate information to achieve the desired behavior
  • if collidable entities don't overlap, no more testing is required
  • if they do overlap, more refined testing is required

Bounding Boxes

Sphere

  • center point and radius (4 numbers for 3D)

Capsule

  • 2D: rectangle and two circles
  • 3D: cylinder and two hemispherical end-caps
  • representation: two points and radius

AABB

  • axis-aligned bounding box
  • rectangular volume (cuboid) whose faces are parallel to the axes of the coordinate system
  • very efficient test for penetration
  • AABB must be recalculated whenever the object rotates

Bounding Boxes

OBB

  • oriented bounding box
  • defined by a position and orientation
  • commonly used

k-DOP

  • discrete oriented polytope
  • more general case of AABB and OBB
  • approximates the shape of an object

Compound shapes

  • more efficient alternative to a poly-soup
  • the system first tests bounding volumes of compound shapes

Convex hull

  • smallest convex volume containing the object

Comparison

Collisions in 2D games

  • even side-scrollers need compound objects
  • simple AABB collision will not work for irregular sprites

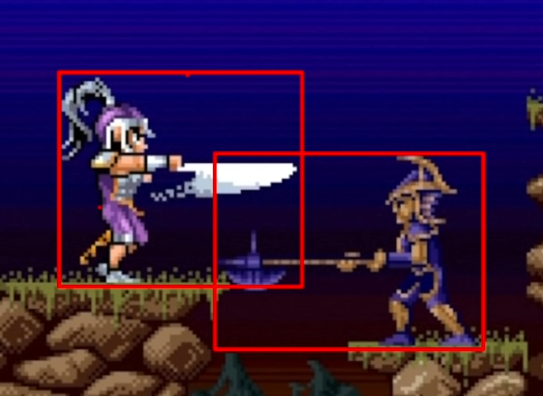
Looking for collision candidates

Naive solution

  • each pair
  • O(n^2)  -> 10 objects result in 100 checks, 100 in 10 000 etc.

Quad-tree

  • efficiency is O(n^{1.5}\log{(n)}) , since the index takes about \log{(n)}  comparisons to traverse
  • good for point-like small objects
  • worst case: n^2

Sweep and Prune

  • sorts the starts (lower bounds) and ends (upper bound) of bounding volumes of each solid along a number of axes

BSP

  • binary space partitioning, good for complex static geometries (buildings)

Grid, Oct-tree, R-tree, R+tree, R*tree, X-tree, M-tree,...

Resolving collision candidates

Sphere-Sphere

  • (C_1 - C_2)\cdot(C_1-C_2) \leq (r_1 + r_2)^2 , where C  is a central point

Sphere-ray

  • we just test the distance between a single sphere center and a ray

AABB-AABB

  • test the borders

AABB-Ray

  • intervals [A, B]  and [C, D]  mustn't overlap

OBB-OBB

  • axis-separating theorem by Gottschalk

SAT

SAT (separating axis theorem)

  • if an axis can be found along which the projection of two
    convex shapes do not overlap, then the two shapes do not intersect
  • for 2D: AABB 2 axes, OBB 4 axes
  • for 3D: AABB 3 axes, OBB 15 axes
  • AABB in 2D: only 2 axis to test

Tunneling problem

Stepped world

  • time steps vary based on occurring situation
  • collision time is calculated by doing binary search in time, moving object back and forth by 1/2 steps (5 iterations is usually enough)

Continuous Collision Detection (CCD)

  • uses Raycasting or more advanced Swept Shapes technique
  • Raycasting - the object emits a ray which is tested for intersection
  • Swept Shapes - a new shape is formed by the motion of the original one

Collision response

How to respond to a collision?

Explosion

  • adding energy to a system of rigid bodies

Fracturing

  • breaking objects apart

Restitution

  • amount of bounce an object has when it hits something
  • when two bodies collide, they compress slightly and then rebound, losing energy

Friction

  • force that arises between two bodies that are in continuous contact, resisting their movement
  • removes energy from a system of rigid bodies
  • static, dynamic, rolling

Constraint

  • taking constraints into consideration (e.g door can only rotate around the hinge)

Collision Resolver

Relaxation

  • LCP - Linear Complementarity Problem
  • if one object moves, it will push another, and another, and another
  • very complex numeric algorithms
  • resolvers: PGS, Dantzig solver, Lemke method, Jacobi method

Coming to rest

  • all objects lose energy, leading to eventual rest
  • not simple (floating-point error, inaccuracies, numerical instability)
    • sleep criteria
      • momentum or energy are below a threshold
    • simulation islands
      • grouping objects that either are interacting or have a potential to interact

Lecture Summary

  • I know basic vector operations: addition, subtraction, magnitude, normalization, and dot product
  • I know basic types of steering behaviors
  • I know object types for physics engines
  • I know what particle systems are
  • I know basic constraints, such as rope, revolute, prismatic, and cone-twist
  • I know basic collision bounding boxes
  • I know SAT theorem
  • I know what CCD is

Goodbye Quote

Do you guys not have phones?Wyatt Cheng, BlizzCon 2018